Brain Test: As you can see from the picture, all you have to do is analyze it and guess who dies if E pushes the stone to the slide on the slope. This fun quiz is sure to boost your cognitive function!
First, you need to keep in mind that the rock will roll down normally despite its crescent shape. Also, keep in mind all the physics and the terrain while you analyze things.
Who Dies if E Pushes The Stone?
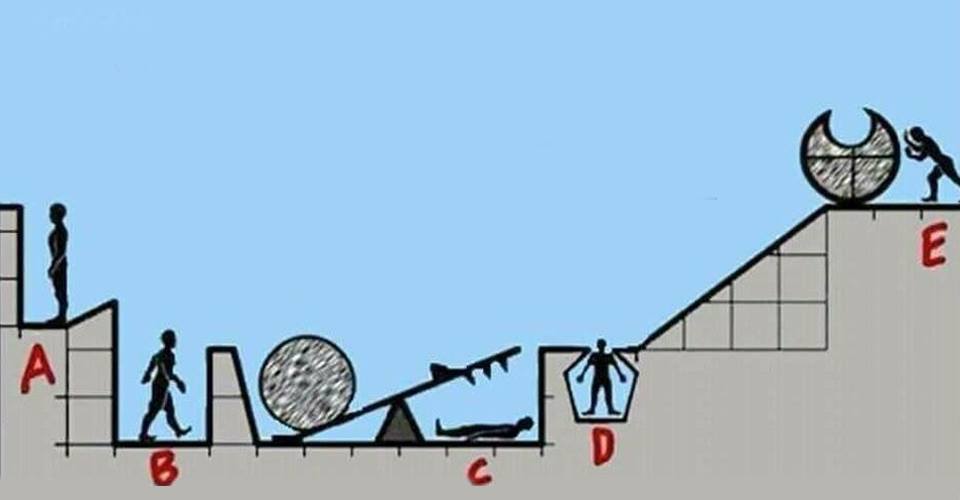
Here are the possible answers to who dies if E pushes the rock in this puzzle:
Answer 1: D and C
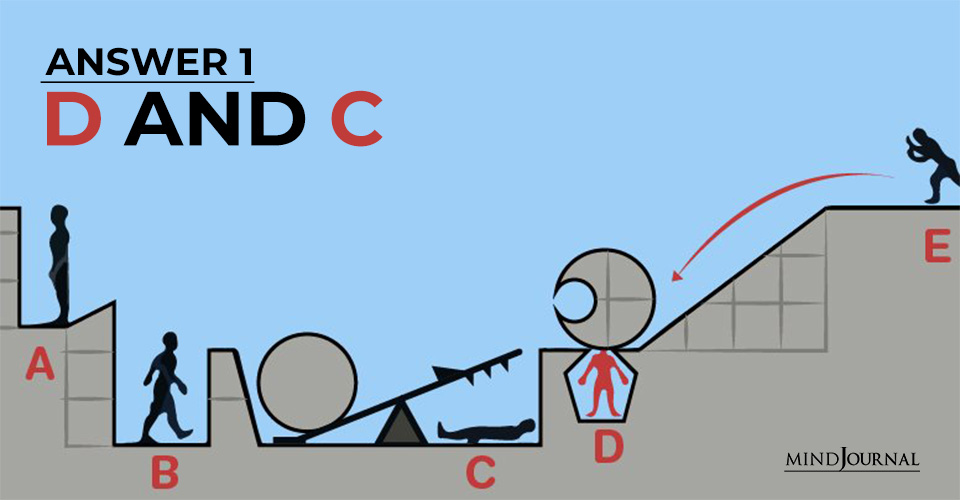
“D” may die first as it clearly appears from the above scene that E has some grudge against D and has planned to kill him. But what if the crescent-shaped stone rolls down and hits the balance under which C is lying? In that case, C may die too (provided the rock is very heavy)!
Related: Which One is Not A Family? Psychological Personality Test
Answer 2: D, C, and E
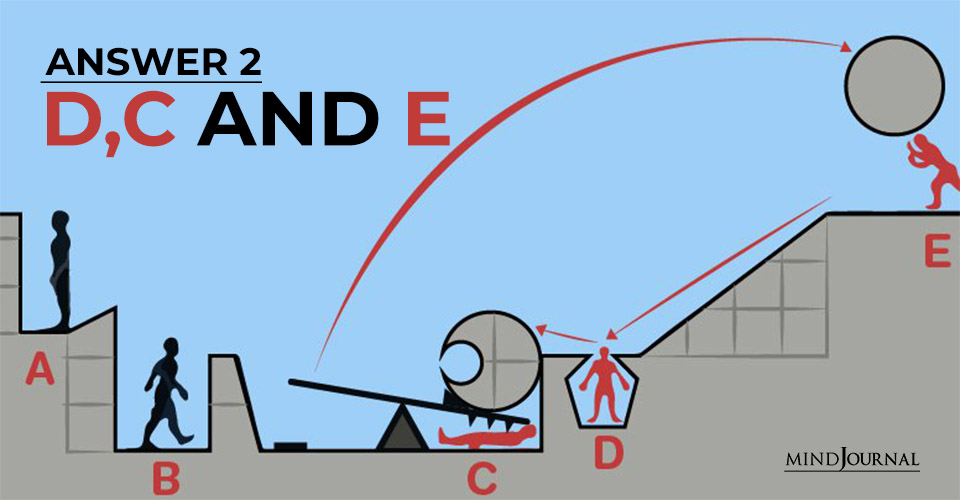
As per the above interpretation if both D and C are killed, then it is highly likely that the first stone pushed by “E” hits the balance, thereby, causing other stones on the balance to jump upwards and hit E in the end.
So, by pushing down one stone, D, C, and E – three are killed. However, this is possible only if the first rock was heavy enough to fling the big rock on the other side of the seesaw.
Answer 3: D, C, and B
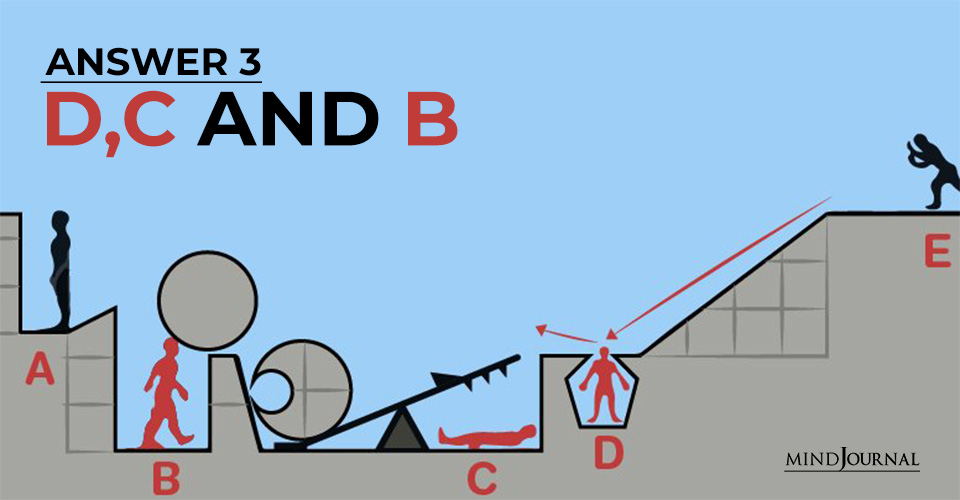
It may also happen that the second stone on the balance surge upwards and hits “B” instead of “E”. If this is true, then there will be three casualties – D, C, and B. But, this is possible only if the rock is heavy enough!
Answer 4: Only D
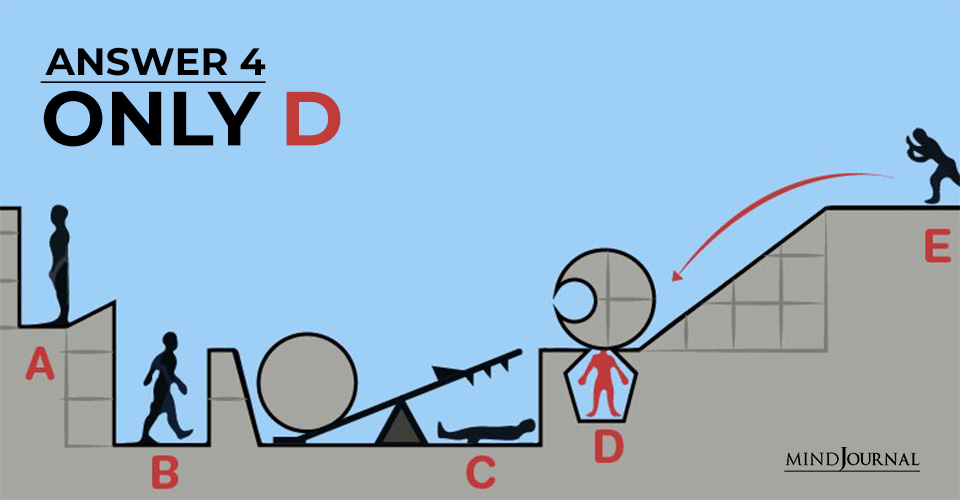
Only D and possibly C die!
Keep in mind that the crescent rock does not have the same mass as the rock on the seesaw. Despite both rocks having the same diameter, the crescent rock has a huge missing section. Therefore, when E rolls down the crescent rock, it will not have enough mass to fling the big rock on the other side of the seesaw.
Related: This Tree Test Reveals Your Dominant Personality Traits
The only other person who could possibly die is C, but that is only if the crescent rock is heavy enough to lower the seesaw’s plank.
Going by the logic, answer 4 is the correct answer!
Did you guess it right as to who dies if E pushes the stone? Let us know in the comments down below.










Leave a Reply
You must be logged in to post a comment.